 download article
download articleFeatures of the centrifugal pump
Article index
 | Q/H curve | |
 | Throttling the flow | |
 | Orifice plate calculation | |
 | Correction of the impeller diameter | |
 | Pump speed control | |
 | Parallely connected pumps | |
 | Pumps connected in series | |
 | Cavitation | |
 | Vapour pressure |
Centrifugal pumps are fluid-kinetic machines designed for power increase within a rotating impeller. Therefore it is also called the hydrodynamic pumping principle.
According to this principle, the fluid is accelerated through the impeller. In the outlet connection of the centrifugal pump, the resulting increase in speed is converted into delivery head. (fig. 1)

Q/H curve
In centrifugal pumps the delivery head H depends on the flow rate Q. This relationship, also called pump performance, is illustrated by curves.
During a bench test, the pump is operated at constant speed and the values Q and H are determined for the various operating points. In order to allow a comparison between the various pump types these measurements are carried out using only water as liquid. With these operating points a Q/H curve be drawn connecting the points on the graph.
Once the flow rate Q is defined and the delivery head H is calculated, the operating point of the plant can be determined. Usually the operating point is not on the Q/H curve of the pump. Depending on the required delivery head, the centrifugal pump will find its operating point when the plant curve and pump curve meet. The flow rate rises from Q1 to Q2. (fig. 2)
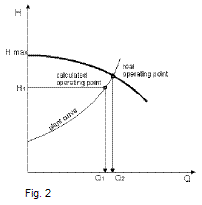
The required operating point is obtained by adapting the pump to the specified operating conditions.
This can be done by the following actions:
Throttling the flow
Partially closing a throttle valve or mounting an orifice plate into the discharge pipe of the pump will increase the pressure drop. The plant curve is shifted.
The operating point B1 (intersection point between pump curve and plant curve) moves on the pump curve to B2. (fig. 3)
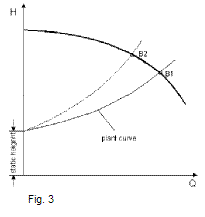
Note: throttling reduces the overall efficiency.
A throttle control or a mounted orifice plate is the less expensive control regarding the investment expenses. In case of significant power requirement, an economic appraisal is highly recommended.
Orifice plate calculation
The friction loss in an orifice plate can be calculated easily:
| ρ [kg/m3] | |
| Δpv = ζ x ρ/2 x (v1)2 x 10-5 | v1 [m/s] |
| pv [bar] |
(fig. 4)
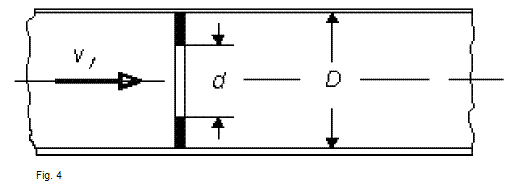
See the values ζ stated in the table below.
| Aperture ratio m = (d/D)2 | Resistance value ζ |
| 0.05 | 800 |
| 0.1 | 250 |
| 0.2 | 50 |
| 0.3 | 20 |
| 0.4 | 4 |
Calculation:
- take the figure stated in the table for d, see table ζ and calculate Δpv .
- if Δpv varies from the required value, take new value for d and calculate once more Δpv.
Correction of the impeller diameter
A correction of the impeller diameter is to be favoured when a permanent reduction of flow rate or differential head is required. The performance of the pump is adjusted towards the duty point by reducing the impeller diameter.
The operating point is shifted from B1 to B2. This is the point where the new pump curve meets the plant curve. (fig. 5)
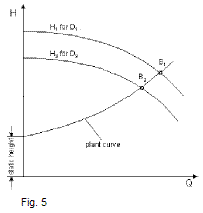
The required impeller diameter can be determined easily using following formulae:
| N = power consumption | ||
| Q1/Q2 ≈ H1/H2 ≈ (D1/D2)2 | N1/N2 ≈ (D1/D2)3 | D = impeller diameter |
| Q = flow rate | ||
| H = total head |
Note: the efficiency of the pump decreases with increasing correction.
Pump speed control
A great number of various operating points can be set continuously, when modifying the pump speed using a variable speed drive or frequency inverter. The operating point moves on the pump curve from B to B2. (fig. 6)
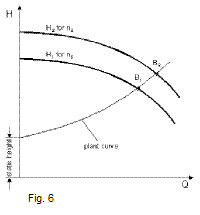
Considering the overall efficiency, this is the best way of flow control. Using a variable speed drive or a frequency inverter additional costs can arise and should be evaluated in an economic appraisal.
The flow rate changes linearly to the speed.
The total head changes with the square of speed.
The power consumption changes with the third power of the speed.
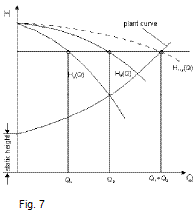
Parallely connected pumps
In the case of pumps connected in parallel the fluid flows are added with corresponding delivery head. This applies to pumps even with different Q/H curve. (fig. 7)
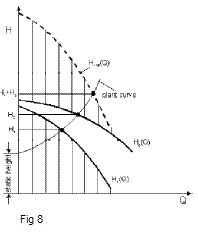
Pumps connected in series
A multistage centrifugal pump performs as single stage pumps connected in series.
Note:
A stationary pump in a system creates a considerable pressure drop. Therefore it is recommendable to install a by pass around pumps which are connected in series.
The overall performance curve of centrifugal pumps connected in series can be calculated by adding the differential head of each pump at the relevant flow rate (- - -). (fig. 8)
Cavitation
Cavitation can be recognised by a strongly increased noise level of the pump with a simultaneous reduced flow rate.
What causes cavitation in centrifugal pumps?
The lowest pressure point in a pump occurs at the inlet of the pump impeller. Due to local pressure reduction part of the fluid may evaporate generating small vapour bubbles. These bubbles are carried along by the fluid and implode instantly when they get into areas of higher pressure. These implosions can create local pressure peaks up to 100.000 bar.
If a pump is cavitating over longer periods, the impeller, the pump housing and cover will wear out. The surface is typically perforated and pitted.
How to avoid cavitation?
Vapour pressure
We should ensure that at all points of the pump, the fluid pressure is higher than the vapour pressure at the corresponding temperature. Take the pressure stated in the vapour-pressure-table of the product to be transferred.
The NPSH value of the plant must be at least 0.5 m higher than the NPSH value of the pump.
For a safe and cavitation free operation the following formula is valid:
NPSHplant > NPSHPump + 0.5 m
The vapour pressure of the product is dependent on the temperature and will rise with increasing temperature.
If the product is pumped at different temperatures the maximum vapour pressure should be used to determine the NPSH value of the plant.
 back to top
back to top


 companies
companies