 download article
download articleFlow behaviour
Article index
 | Dynamic viscosity η | |
 | Flow behaviour of fluids | |
 | Ideal viscous flow behaviour: | |
 | Pseudoplastic flow behaviour: | |
 | Irreversible flow behaviour: | |
 | Types of flow | |
 | Laminar flow | |
 | Turbulent flow | |
 | Reynolds number |
Dynamic viscosity η
Looking at two parallel plates with the surface A and the distance y, displaced against each other as a result of a force Faction with a velocity v, a force Freaction opposes to this displacement and increases with increasing dynamic viscosity of the medium between the two plates. (fig 1)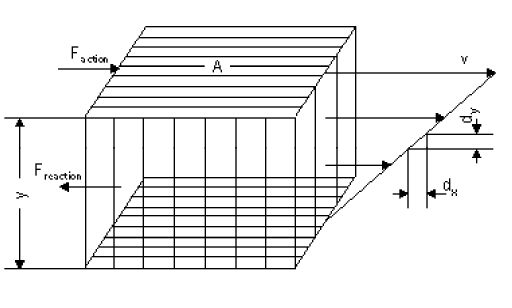
The ratio of F to A is called shear stress τ.
τ = F / A
The shear stress τ increases in proportion to the shear velocity D and the dynamic viscosity η.
τ = D x η
The ratio of v to y is defined as shear velocity D.
D = v / y
Thus the resulting dynamic viscosity η:
η = τ / D
Thus, the dynamic viscosity η is a characteristic parameter of the fluid concerned and depends on the temperature. Therefore the viscosity is always indicated together with the corresponding temperature.
Flow behaviour of fluids
Ideal viscous flow behaviour:
Fluids with an ideal viscous flow behaviour are called Newtonian fluids. They are viscous fluids with linear molecules. They show a proportional flow behaviour. (fig 2)
Typical Newtonian fluids are: water, salad oil, milk, sugar solutions, honey.
Pseudoplastic flow behaviour:
The flow behaviour of fluids depends on their physicochemical properties. Adding a filling agent to a pure solvent, will increase the viscosity and change the flow behaviour.With increasing shear stress, in general the viscosity of highly molecular products in solutions and melts tends to decrease.
Such a flow behaviour is called pseudoplastic. (fig 3)
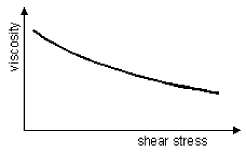
Examples of pseudoplastic flow behaviour: condensed milk, orange juice.
Irreversible flow behaviour:
Fluids deformed under applied shear stress in a way that the structure after the destructive phase (shear time) can not be restored show an irreversible flow behaviour.The result is a permanent, shear time dependent change of viscosity. (fig 4)
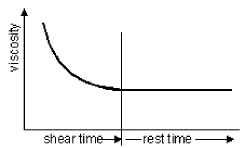
Example for irreversible flow behaviour: Yoghurt.
Types of flow
Depending on the Reynolds number, the flow passing through a pipe shows specific, typical flow patterns with different physical properties.In this context the generation of a laminar or turbulent flow is of particular concern.
Laminar flow
In case of a laminar flow, the particles move in a streamline form and parallely to the pipe axis without being mixed. (fig 5)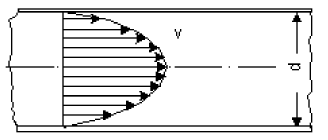
The roughness of the inside wall of pipes has no effect on the friction loss.
You will find a laminar flow mainly with high viscous fluids.
The loss of head changes linearly with the flow velocity.
Turbulent flow
In case of a turbulent or vortical flow the particles are mixed because of the movement along the pipe axis and an additional, transverse movement. (fig 6)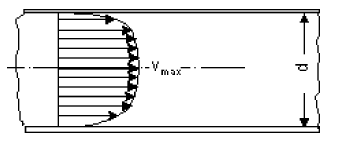
The roughness of the pipe inside has great effect on the friction loss.
Turbulent flows are mainly found with water or fluids similar to water.
The loss on pump head varies by square of the flow velocity.
Reynolds number
The Reynolds number describes the correlation between the flow velocity v, the viscosity η and the inner diameter of the pipe di.The Reynolds number has no dimension.
Re = (v * d * ρ) / η
Flow velocity v [m/s]
Viscosity η [Pa s]
Inner pipe diameter di [mm]
Density ρ [kg/dm3]
Viscosity η [Pa s]
Inner pipe diameter di [mm]
Density ρ [kg/dm3]
With a Reynolds number of 2320 the laminar flow passes to a turbulent flow.
Example:
In one second, 2 litres of acetic acid passes through a pipe with a nominal bore of 50 mm.
The acetic acid has a dynamic viscosity of η = 1.21 mPa s = 0.00121 Pa s and a density of 1.04 kg/dm3.
Is the flow laminar or turbulent?
The average flow velocity amounts to:
| Q [l/s] | |
| v = Q / A = Q / (¼ πd2) = (2 * 1000) / (502 * π / 4) = 1.02 m/s | d [mm] |
| v [m/s] |
Thus the calculated Reynolds number is:
Re = (v * d * ρ) / η = (1.02 * 50 * 1.04) / 0.00121 = 43834
The Reynolds number exceeds the critical Reynolds number Rekrit=2320. The flow is turbulent.
 back to top
back to top


 companies
companies