This article is not yet available in the language you selected
Ohmic and Inductive Heating
Article index
Scope of Deliverables
This section covers information, where available, on kinetics and relevant safety considerations for processing commercially sterile or extended shelf-life products produced by ohmic and inductive heating. It does not include combinations of other alternate process technologies with ohmic and inductive heating, since the number of potential combinations is infinite but no information is available.
1. Introduction
1.1. Definition, Description and Applications
Ohmic heating (sometimes also referred to as Joule heating, electrical resistance heating, direct electrical resistance heating, electroheating, and electroconductive heating) is defined as a process wherein (primarily alternating) electric currents are passed through foods or other materials with the primary purpose of heating them. The heating occurs in the form of internal energy generation within the material. Ohmic heating is distinguished from other electrical heating methods either by the presence of electrodes contacting the food (as opposed to microwave and inductive heating, where electrodes are absent), frequency (unrestricted, except for the specially assigned radio or microwave frequency range), and waveform (also unrestricted, although typically sinusoidal).
In inductive heating, electric coils placed near the food product generate oscillating electromagnetic fields that send electric currents through the food, again primarily to heat it. Such fields may be generated in various ways, including the use of the flowing food material as the secondary coil of a transformer. Inductive heating may be distinguished from microwave heating by the frequency (specifically assigned in the case of microwaves), and the nature of the source (the need for coils and magnets for generation of the field, in the case of inductive heating, and a magnetron for microwave heating).
Information on inductive heating is extremely limited. A project was conducted in the mid-1990s at the Technical University of Munich (Rosenbauer 1997), under sponsorship from the Electric Power Research Institute. No data about microbial death kinetics under inductive heating were published. Thus, the succeeding discussion focuses on ohmic heating.
A large number of potential future applications exist for ohmic heating, including its use in blanching, evaporation, dehydration, fermentation, and extraction. The present discussion, however, concerns primarily its application as a heat treatment for microbial control. In this sense, the main advantages claimed for ohmic heating are rapid and relatively uniform heating. Ohmic heating is currently being used for processing of whole fruits in Japan and the United Kingdom. One commercial facility in the United States uses ohmic heating for the processing of liquid egg.
The principal advantage claimed for ohmic heating is its ability to heat materials rapidly and uniformly, including products containing particulates. This is expected to reduce the total thermal abuse to the product in comparison to conventional heating, where time must be allowed for heat penetration to occur to the center of a material and particulates heat slower than the fluid phase of a food. In ohmic heating, particles can be made to heat faster than fluids by appropriately formulating the ionic contents of the fluid and particulate phase to ensure the appropriate levels of electrical conductivity.
1.2. Summary of Mechanisms of Microbial Inactivation
The principal mechanisms of microbial inactivation in ohmic heating are thermal in nature. Occasionally, one may wish to reduce the process requirement or to use ohmic heating for a mild process, such as pasteurization. It may then be advantageous to identify additional non-thermal mechanisms. Early literature is inconclusive, since temperature had not been completely eliminated as a variable. Recent literature that has eliminated thermal differences, however, indicates that a mild electroporation mechanism may occur during ohmic heating. The principal reason for the additional effect of ohmic treatment may be its low frequency (50 - 60 Hz), which allows cell walls to build up charges and form pores. This is in contrast to high-frequency methods such as radio or microwave frequency heating, where the electric field is essentially reversed before sufficient charge buildup occurs at the cell walls.
1.3. Summary of Microbial Inactivation Kinetics
A summary of the available kinetic data is presented in Tables 1 through 3 in Section 3.4. While some evidence exists for non-thermal effects of ohmic heating, a larger body of research is needed to understand more fully the mechanisms for microbial inactivation. For most ohmic processes, which rely on heat, it may be unnecessary for processors to claim this effect in their process filings; however, if sufficient data is available, it may be possible for future processes to be reduced.
1.4. Summary of Critical Process Factors
Temperature is the principal critical process factor in ohmic heating. As in conventional thermal processes, the key issue is determining the zone(s) of minimum thermal treatment. Fundamentally, there is only 1 critical factor: temperature-time history of the coldest point. Temperature of an ohmic process, however, is significantly affected by other factors, which will be discussed in greater detail in section 4.1.
1.5. Other Considerations
While it is possible to envision creative combinations between ohmic heating and other alternative process technologies, no data are available at this time.
2. Pathogens of Public Health Concern Most Resistant to the Technology
2.1. Identification of Pathogens Resistant to Ohmic Heating
Since the purpose of this technology is to use the rapid, volumetric heating provided by the electrothermal methods, the most resistant pathogens would likely be the same as those for thermal processes. Results to date show that the electric field can only enhance microbial kill, so any additional beneficial effect will add an extra factor of safety.
2.2. Effects of the Critical Process Factors on Inactivation
Since the main critical process factor is the thermal history and location of the cold spot, the effects on microbial inactivation are the same as for thermal processes. Locating cold zones during ohmic heating, however, cannot be extrapolated from current knowledge of conventional heating and requires special consideration.
2.3. Shape of Inactivation Curve
Microbial inactivation curves of ohmic heating processes are similar to thermal curves, except for differences in slope (the rate may be enhanced by the electric field) on some occasions. Thus, the conventional D- and z-value kinetics, (or, alternatively, rate constants and activation energies) are relevant. These are summarized in Section 3.4.
3. Mechanisms of Inactivation
3.1. Pathogen Culture Maintenance
A review of the literature describing the application of ohmic processing to foods revealed that there are no particular pathogen strains with a unique resistance to the technology. Again, since the predominant method of microbial inactivation is thermal, thermal death kinetics of pathogens and target spoilage organisms would be followed. Therefore, standard published and generally accepted preparing and culturing procedures (National Canners Association 1968) should be used for pathogenic, surrogate cultures or spores in order to evaluate an ohmic processing unit's ability to inactivate them. Depending on the case, culture maintenance will be done either by in-house trained staff or by outside consulting firms that will provide materials for testing and system validation. As a rule, a surrogate should have the highest heat resistance recognized for that type of microorganism. A biological test culture with sub-standard heat resistance is of little use in evaluating a thermal process. For a detail discussion of the characteristics of surrogate microorganisms, see Overarching Principles Section 4.
Once the key pathogen(s) are selected and the surrogates for them identified, literature and experts in the field can help identify suitable culture maintenance and preparation conditions for a process evaluation.
3.2. Microbial Enumeration Conditions and Methods
See Overarching Principles Section 2.
3.3. Detailed Analysis of Inactivation Mechanism(s) for Pathogens Identified, as a Function of Process Variables, Microbial Repair and Regeneration, and Effects of Post-processing Storage
Because the principal mechanisms of microbial inactivation are thermal in nature, processors intending to file ohmic treatment processes with FDA should be able to file processes based on thermal inactivation. At times, one may wish to reduce the process requirement or to use ohmic heating as a mild processing method, such as pasteurization. It may then be advantageous to determine if additional non-thermal mechanisms exist.
Early literature on non-thermal effects has been inconclusive (Palaniappan and others 1990). Most studies either did not specify sample temperatures or failed to eliminate temperature as a variable. It is critically important that any studies comparing conventional and ohmic heating are conducted under similar temperature histories. Palaniappan and Sastry (1992) found no difference between the effects of ohmic and conventional heat treatments on the death kinetics of yeast cells (Zygosaccharomyces bailii), under identical histories. In some cases, however, a mild electrical pretreatment of Escherichia coli decreased the subsequent inactivation requirement.
More recent studies suggest that a mild electroporation mechanism may contribute to cell inactivation during ohmic heating. For example, studies on fermentation of Lactobacillus acidophilus under the presence of a mild electric field (Cho and others 1996) have indicated that although the fermentation lag phase can be significantly reduced, the productivity of the fermentation is also lowered by the presence of the electrical field. This may be due to the presence of mild electroporation, which improves the transport of substrates at the early stages of fermentation, thereby accelerating it. At the later stages, the electroporation effect would improve the transport of metabolites into the cell and thereby would inhibit fermentation. The presence of pore-forming mechanisms on cellular tissue has been confirmed by recent work (Imai and others 1995; Wang 1995; Kulshrestha and Sastry 1999). Another recent study (Cho and others 1999), conducted under near-identical temperature conditions, indicates that the kinetics of inactivation of Bacillus subtilis spores can be accelerated by an ohmic treatment. A 2-stage ohmic treatment (ohmic treatment, followed by a holding time prior to a second heat treatment) further accelerated death rates. A recent study (Lee and Yoon 1999) has indicated that leakage of intracellular constituents of Saccharomyces cerevisiae was enhanced under ohmic heating, as compared to conventional heating in boiling water.
The principal reason for the additional effect of these ohmic treatments may be the low frequency (50 - 60 Hz) used, which allows cell walls to build up charges and form pores (electroporation mechanism). This is in contrast to high-frequency methods such as radio or microwave frequency heating, where the electric field is essentially reversed before sufficient wall charge buildup occurs. Some contrary evidence has also been noted. In particular, the work of Lee and Yoon (1999) has indicated that greater leakage of S. cerevisiae intracellular constituents is detected under high frequencies. The details of temperature control within this study, however, are not available at this time, so it is not known if these researchers had adequately eliminated temperature effects.
Little or no information is available regarding the effects on survivor counts from ohmic heating processes on post-processing storage. In 1 industry study, survivor counts in a pasteurized liquid egg product decreased over storage time, apparently due to injury effects (Reznik 1999). In this study, initial post-pasteurization plate counts from conventional (plate) and electroheating were similar; however, after 12 wk of storage, many conventionally heated samples were reported to reach counts of 10,000 cfu/ml, while the electroheated samples exhibited less than 10 cfu/ml in most samples. No detailed statistical information on this study is available.
3.4. Description of Methods to Measure or Mathematically Model Pathogen Inactivation
A summary of the available kinetic data of microbial inactivation is presented in Tables 1 through 3.
While some evidence exists for non-thermal effects of ohmic heating, a larger body of research is needed to understand more fully the inactivation mechanism of the various microorganisms. For most ohmic processes, which rely on heat, it may be unnecessary for processors to claim this effect in their process filings; however, future processes may be reduced, if sufficient data are available.
Table 1. D-values and kinetic reaction rate constants (k) for Bacillus subtilis spores under conventional and ohmic heating (Cho and others 1999).
|
Temperature (°C) |
D-values, conventional heating (min-1) |
D-values, ohmic heating (min-1) |
k, conventional heating (s-1) |
k, ohmic heating (s-1) |
|
88 |
32.8 |
30.2 |
0.00117 |
0.001271 |
|
92.3 |
9.87 |
8.55 |
0.003889 |
0.004489 |
|
95 |
5.06 |
0.007586 |
||
|
95.5 |
4.38 |
0.008763 |
||
|
97 |
3.05 |
0.012585 |
||
|
99.1 |
1.76 |
0.021809 |
||
|
z-value (°C) or Activation energy (Ea)(kcal/mol) |
8.74* |
9.16* |
70.0** |
67.5** |
* - z-value; ** - Activation Energy
Table 2. D-values and reaction rate constants for inactivation of Bacillus subtilis spores during single and double stage conventional and ohmic heating at 90 °C (Cho and others 1999).
|
Stage # |
D-values, conventional heating (min-1) |
D-values, ohmic heating (min-1) |
k, conventional heating (s-1) |
k, ohmic heating (s-1) |
|
1 |
17.1 |
14.2 |
0.002245 |
0.002703 |
|
2 |
9.2 |
8.5 |
0.004172 |
0.004516 |
Table 3. Kinetic reaction rate constants (k) for Zygosaccharomyces bailii under conventional and ohmic heating (Palaniappan and others 1992).
|
Temperature (°C) |
D-values, conventional heating (min-1) |
D-values, ohmic heating (min-1) |
k, conventional heating (s-1) |
k,ohmic heating (s-1) |
|
49.8 |
294.6 |
274.0 |
0.008 |
0.009 |
|
52.3 |
149.7 |
113.0 |
0.016 |
0.021 |
|
55.8 |
47.21 |
43.11 |
0.049 |
0.054 |
|
58.8 |
16.88 |
17.84 |
0.137 |
0.130 |
|
z-values (°C) or Activation energy (Ea) (kcal/mol) |
7.19* |
7.68* |
29.63** |
27.77** |
* - z-value; ** - Activation Energy
4. Validation/Critical Process Factors
4.1. Identification and Description of Critical Process Factors
Since ohmic heating is fundamentally a thermal-based process, temperature and time are the principal critical process factors. Ohmic heating is an internal energy generation process, so there is theoretically no upper temperature limit to the process. Thus, if product hold-up occurs, it is possible for boiling to occur within the system even with a high degree of pressurization.
As in conventional thermal processes, the key problem is locating the zone(s) of minimum thermal treatment. Fundamentally, then, there exist only 2 critical factors, temperature and time of treatment at the coldest zone(s).
Several other factors, however, significantly affect the temperature within an ohmic process. Within a continuous flow ohmic heating system, the critical parameters affecting ohmic heating include the electrical conductivity(ies) of the respective phases of the food, the temperature dependence of electrical conductivity, the design of the heating device, the extent of interstitial fluid motion, the residence time distribution (if any), thermophysical properties of the food, and electric field strength. Although 2 commercial manufacturers currently produce ohmic systems, no standard or preferred designs are available. Therefore, while a detailed treatment of these factors cannot be attempted within the scope of this document, some general comments may be made.
The rate of heating is directly proportional to the square of the electric field strength, E, and the electrical conductivity, σ (Sastry 1994). Since the electrical conductivity of most foods increases with temperature (Palaniappan and Sastry 1991a, 1991b; Halden and others 1990), ohmic heating becomes more effective as temperature increases; however, this also raises the possibility of runaway heating, (similar to microwaves), and the possibility of arcing due to deposition of proteinaceous material on electrode surfaces. Another major factor affecting electrical conductivity is ionic content. It is therefore possible to formulate products with salt levels designed for effective ohmic heating. The electric field strength may be varied either by changing the electrode gap or the applied voltage, although the latter is much more easily controlled for any given design.
Other product properties that may effect temperature distribution include the density and specific heat of the food product. High densities and specific heats are conducive to slower heating. The thermal conductivity of the food may be of relevance if the material is heterogeneous, but is of relatively low importance for homogeneous materials.
Equipment design is another critical factor that should be considered. Some of the designs that are commercially available include electrodes that are located at various positions along the length of the product flow path (in-line field), or those located perpendicular to the flow (cross-field). The considerations in each of these cases are somewhat different. In the in-line field design, the device generally operates at high voltage and relatively low current. The product heats as it flows through the heater, so its electrical conductivity changes over the length. Since the total voltage drop in the heater must equal the applied voltage, the material at the upstream end experiences high field strengths, and downstream locations experience lower field-strengths. In the cross-field design, the field strength is constant throughout the system. While these are basic designs, a number of other possibilities exist, or are in development at this time; thus, it is not possible to present a comprehensive discussion here.
As in other thermal processes, it is necessary to identify the location(s) of cold zones and their motion. The thermal process must be sufficient to inactivate target pathogens to the desired extent at the location(s) of least lethal treatment. For a homogeneous fluid medium, such a position would likely be at the fastest moving region.
For the processing of solid-liquid mixtures, the question of the location of least lethal treatment has received considerable attention. Modeling work (de Alwis and Fryer 1990a,b; de Alwis and others 1989; Fryer and others 1992; Fu and Hsieh 1999), conducted for a static system, showed the effects of differences in electrical conductivity between a single low- or high-conductivity particle (inclusion particle) located within a medium of significantly different electrical conductivity. Sastry (1992) and Sastry and Palaniappan (1992) showed that the less conductive phase could heat faster than the fluid, if it was present in sufficiently high concentration. They also noted that an inclusion particle may provide a worst-case scenario. Since that time, considerable effort has gone into determining the worst-case scenario within an ohmic processing system (Zhang and Fryer 1993; Sastry and Salengke 1998). Unlike conventional heating systems, it is not clear that the worst case is necessarily associated with a static situation. Indeed, Khalaf and Sastry (1996) and Sastry and Salengke (1998) indicated that in situations where the solid is less conductive than the fluid, the worst case is associated with a well-mixed fluid surrounding the solid; however, when the solid phase is more conductive than the fluid, the worst case appeared to be the static condition. Further studies by Salengke and Sastry (1999) show that, when the situation favors a cold spot within the solid phase, the worst-case occurs with a well-mixed fluid (Fig. 1), but when the cold-spot occurs within the fluid phase, the worst case is static (Fig. 2). Davies and others (1999) have shown the effects of shadow formation around individual solid particles, under a static condition in 2 dimensions.
As the above discussion suggests, 1 critical factor is likely to be fat content. If a fat globule is present within a highly electrical conductive region, where currents can bypass the globule, it may heat slower than its surroundings due to its lack of electrical conductivity. Under such conditions, any pathogens potentially present within the fat phase may receive less treatment than the rest of the product. Heating of the fat phase may then depend on the rate at which energy is transferred from the surroundings. Based on the foregoing discussion, a high heat transfer coefficient may not necessarily relate to the worst case, since fluid motion tends to moderate heating in such situations. If a fat-rich (low conductivity) phase is aligned to significantly intercept the current, it is possible for such a zone to heat faster than the surrounding fluid. In any case, care must be taken in establishing the process.
Whatever the scenario under consideration, the worst-case must be accounted for. Particle electrical conductivity and its temperature dependence are critical control factors that define the worst-case scenario. Additionally, the cold zone may shift considerably during the course of processing, depending on the relative electrical conductivities of phases. The exact details are likely to be equipment-specific; thus, a separate analysis may need to be conducted for each new system and product.
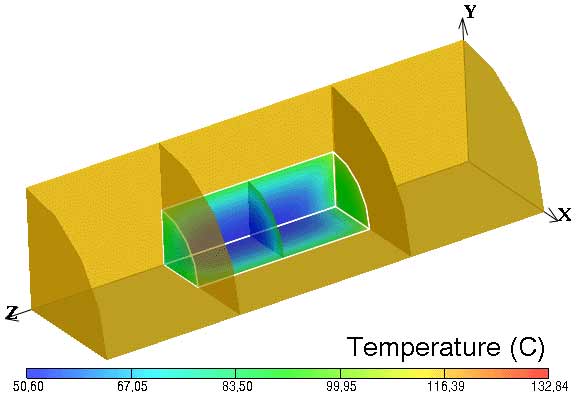
(a)
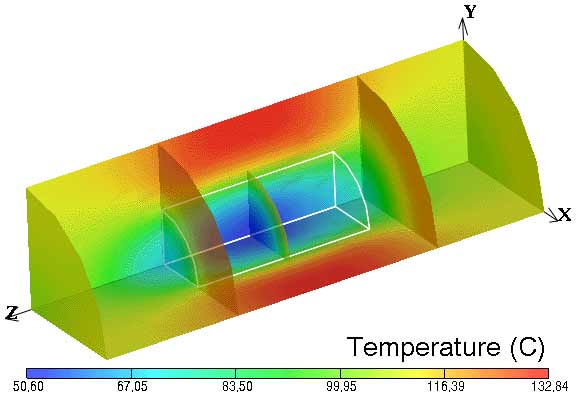
(b)
Figure 1. Color mapping of modeled temperature distributions within an ohmic heater after 150 s of ohmic heating, for a single solid cylindrical "inclusion" particle 1/3 as conductive as the fluid; (a) well-mixed fluid (b) static fluid.
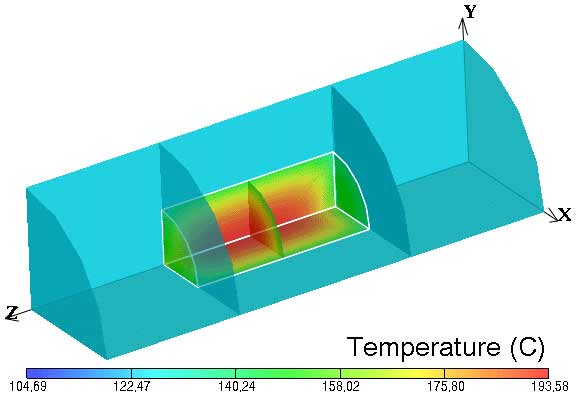
(a)
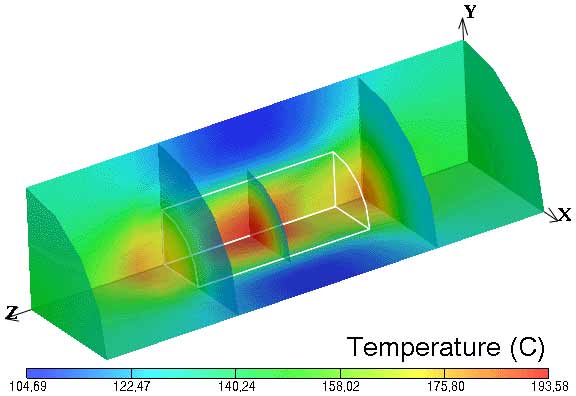
(b)
Figure 2. Color mapping of modeled temperature distributions within an ohmic heater after 150 s of ohmic heating, for a single solid cylindrical "inclusion" particle twice as conductive as the fluid; (a) well-mixed fluid (b) static fluid.
4.2. Describe Methods to Measure/Monitor Critical Process Factors
For single-phase homogeneous fluid foods, temperature may be monitored at the cold zone, which may typically be the fastest-moving region of fluid. Temperature measurements are complicated by the presence of an electrical field; thus, the temperature sensor must be electrically isolated from the surrounding environment. An example of such isolation is a teflon-coated thermocouple.
Currently, there is no physical method available for measurement of temperature within real particulate food products undergoing continuous ohmic heating. Measurements have been conducted with liquid crystal (Sastry and Li 1996), which works only for transparent foods, and MRI (magnetic resonance imaging) (Ruan and others 1999), which is limited by the need to turn off the electrical field for 14 s during data acquisition.
The only other approach appears to be the use of history indicators (time temperature integrators), either biological (microbiological or enzymatic) or chemical. The same principles as thermal processing apply and extra care should be given to critical factors associated with the ohmic heating process (the presence of the indicator should not influence the heating process). For recent reviews on time temperature integrators, see Hendrickx and others (1995) and Van Loey and others (1996). An application to ohmic heating has recently been described by Kim and others (1996). If the worst-case scenario for a product could be pre-established by mathematical models, it would be possible to evaluate total process treatment by such indicators.
4.3. Description of Microbial or Chemical Surrogates/Indicators
To determine processing kinetics and efficiency of ohmic inactivation of microorganisms, a surrogate/indicator organism would be selected from those microbes traditionally used in thermal processing studies. No organism(s) with unique resistance to ohmic processing has been reported in the literature, suggesting that classical surrogates (vegetative cells or spores) would be appropriate for process determination and validation (see Overarching Principles Section 2).
5. Process Deviations and How to Handle Them
Process deviations in this technology are equipment-specific. Since no standard equipment design currently exists, the character of the deviation and the corrective action cannot be characterized in a simple manner within the scope of this document.
5.1. Basic Detection Methods for Process Deviations
Depending on the system, the detection methods may involve monitoring of particle conductivities, system power input, and inlet and outlet temperatures. Significant deviations from operating conditions may indicate an abnormality that is equipment-specific. Further, it is important to protect against undetectable hazards.
One approach to preventing process deviations would be to monitor electrical conductivity of the process stream on-line. Solids of unusually low or high electrical conductivity could be detected, in principle, and diverted before entering the heater; however, much depends on the sensitivity of the detection technique and the background noise created by natural variations in product electrical conductivity.
5.2. Methods to Assess and Correct Deviations
Assessing and correcting deviations is not simple, since the knowledge base is incomplete at this time. As stated above, this is a subject that needs further research and separate, design-specific evaluation. If deviations occur beyond the safety factors set by design, then complete product reprocessing may be necessary. As stated above, the information will depend on design, and insufficient information is available at this time.
6. Research Needs
The following areas of research need to be addressed before implementing ohmic heating as a preservation method:
- Develop a more complete body of knowledge about the combined influence of temperature and electric fields on the destruction kinetics of key pathogenic microorganisms.
- Develop the knowledge base to assess the impact of deviations for specific designs of ohmic heaters. This would include improved models for ohmic processes.
- Develop methods for monitoring temperatures within individual solids.
GLOSSARY
A complete list of definitions regarding all the technologies is located at the end of this document.
Conductivity (Electrical), σ. Physical property of a food material that determines its ability to conduct electricity and is expressed in Siemens per cm (S/cm). In ohmic heating, it enables heating to occur.
Conductivity (Thermal). Physical property of a food material which determines its ability to conduct heat. Expressed in Watts/meter oC.
Conventional heating. Heating of a substance by transfer of thermal energy from a heating medium to a low temperature product.
Cross-field. An ohmic heating system where the electric field is aligned across the product flow path.
Electroheating. See ohmic heating
Inclusion particle. A food particle of significantly different electrical conductivity than its surroundings.
Interstitial fluid motion. The motion of fluid in the spaces between solid particles.
Non-thermal effects. Effects due to the exposure to a process that are not of thermal origin, i.e., cannot be explained by measured temperature changes.
Specific heat. The ability of a material to store heat. Described technically as the amount of energy required to raise the temperature of unit mass of an object by a unit increment in temperature.
Thermophysical properties. Properties that influence the heating rate of a material. Examples of thermophysical properties are thermal conductivity (the ability of the material to conduct heat), specific heat (the ability of the material to store heat), and density (the mass per unit volume of the material).
REFERENCES
Cho, H.-Y., Sastry, S. K. and Yousef, A. E. 1996. Growth kinetics of Lactobacillus acidophilus under ohmic heating. Biotechnol Bioeng. 49(3):334-340
Cho, H.-Y., Sastry, S. K. and Yousef, A. E. 1999. Kinetics of inactivation of Bacillus subtilis spores by continuous or intermittent ohmic and conventional heating. Biotechnol Bioeng. 62(3):368-372
Davies, L. J., Kemp, M. R. and Fryer, P. J. 1999. The geometry of shadows: effects of inhomogeneities in electrical field processing. J Food Eng. 40:245-258
de Alwis, A. A. P., Halden, K. and Fryer, P. J. 1989. Shape and conductivity effects in ohmic heating of foods. Chem Eng Res Des. 67:159-168
de Alwis, A. A. P. and Fryer, P. J. 1990a. A finite element analysis of heat generation and transfer during ohmic heating of food. Chem Eng Sci. 45(6):1547-1559
de Alwis, A. A. P. and Fryer, P. J. 1990b. The use of direct resistance heating in the food industry. J Food Eng. 11:3-27
Fryer, P. J., de Alwis, A. A. P., Koury, E., Stapley, A. G. F. and Zhang, L. 1992. Ohmic processing of solid-liquid mixtures: heat generation and convection effects. J Food Eng. 18:101-125
Fu, W.-R. and Hsieh, C.-C. 1999. Simulation and verification of 2-dimensional ohmic heating in static system. J Food Sci. 64(6):946-949
Halden, K., de Alwis, A. A. P. and Fryer, P. J. 1990. Changes in the electrical conductivity of foods during ohmic heating. Int J Food Sci Technol. 25:9-25
Hendrickx, M., Maesmans, G., De Cordt, S., Van Loey, A., Noronha, J. and Tobback, P. 1995. Evaluation of the integrated time-temperature effect in thermal processing of foods. CRC Critical Reviews in Food Science and Nutrition. 35(3):231-262
Imai, T., Uemura, K., Ishida, N., Yoshizaki, S. and Noguchi, A. 1995. Ohmic heating of japanese white radish Rhaphanus sativus. Int J Food Sci Technol. 30:461-472
Khalaf, W. G. and Sastry, S. K. 1996. Effect of fluid viscosity on the ohmic heating rate of solid-liquid mixtures. J Food Eng. 27:145-158
Kim, H. J., Choi, Y.-M., Yang, T. C. S., Taub, I. A., Tempest, P., Tucker, G. and Parrott, D. L. 1996. Validation of ohmic heating for quality enhancement of foods products. Food Technol. 50(5):253-261
Kulshrestha, S. A. and Sastry, S. K. 1999. Low-frequency dielectric changes in vegetable tissue from ohmic heating. IFT Annual Meeting: Book of Abstracts. p. 211. Chicago, IL.
Lee, C. H. and Yoon, S. W. 1999. Effect of ohmic heating on the structure and permeability of the cell membrane of saccharomyces cerevisiae. 1999 IFT Annual Meeting. Chicago. July 24-28 1999.
National Canners Association 1968. Laboratory manual for food canners and processors. AVI Publishing Company. 1. 1-8, 94-100.
Palaniappan, S., Richter, E. R. and Sastry, S. K. 1990. Effects of electricity on microorganisms: A review. J Food Process Preserv. 14:393-414
Palaniappan, S. and Sastry, S. K. 1991a. Electrical conductivity of selected solid foods during ohmic heating. J Food Process Eng. 14:221-236
Palaniappan, S. and Sastry, S. K. 1991b. Electrical conductivity of selected juices: influences of temperature, solids contact, applied voltage and particle size. J Food Process Eng. 14:247-260
Palaniappan, S. and Sastry, S. K. 1992. Effects of electroconductive heat treatment and electrical pretreatment on thermal death Kinetics of selected microorganisms. Biotechnol Bioeng. 39(2):225-232
Reznik, D. L. 1999. Personal communication. Raztek Corp, Sunnyvale, CA.
Rosenbauer, G. 1997. Continuous induction heating of liquids. Research Institute for Food Technology and Utilization, Technical University of Munich. Unpublished.
Ruan, R., Chen, P., Chang, K., Kim, H.-J. and Taub, I. A. 1999. Rapid food particle temperature mapping during ohmic heating using FLASH MRI. J Food Sci. 64(6):1024-1026
Salengke, S. and Sastry, S. K. 1999. Comparative modeling study of ohmic heating of solid-liquid mixtures. 1999 IFT Annual Meeting. Chicago. July 24-28 1999.
Sastry, S. K. 1992. A model for heating of liquid-particle mixtures in a continuous flow ohmic heater. J Food Process Eng. 15:263-278
Sastry, S. K. and Palaniappan, S. 1992. Mathematical modeling and experimental studies on ohmic heating of liquid-particle mixtures in a static heater. J Food Process Eng. 15:241-261
Sastry, S. K. 1994. Ohmic heating. R. P. Singh and F. A. R. Oliveira. Minimal Processing of Foods and Process Optimization: an Interface. Boca Raton, FL. CRC Press, Inc. 17-33.
Sastry, S. K. and Li, Q. 1996. Modeling the ohmic heating of foods. Food Technol. 50(5):246-248
Sastry, S. K. and Salengke, S. 1998. Ohmic heating of solid-liquid mixtures: a comparison of mathematical models under worst-case heating conditions. J Food Process Eng. 21:441-458
Van Loey, A., Hendrickx, M., De Cordt, S., Haentjens, T. and Tobback, P. 1996. Quantative evaluation of thermal process using time temperature integrators. Trends Food Sci Technol. 7(1):16-26
Wang, W.-C. 1995. Ohmic heating of foods: physical properties and applications. Columbus, OH. The Ohio State University.
Zhang, L. and Fryer, P. J. 1993. Models for the electrical heating of solid-liquid mixtures. Chemical Engineering Science. 48:633-643
U. S. Food and Drug Administration
Center for Food Safety and Applied Nutrition
June 2, 2000
 back to top
back to top



 companias
companias